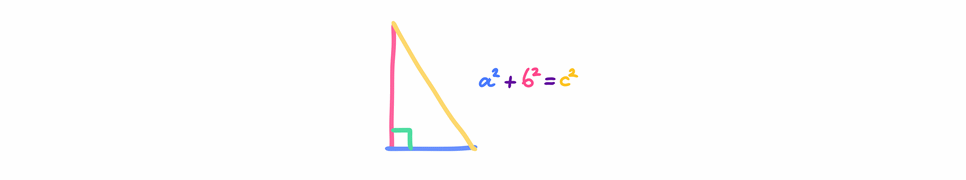Pythagorean Theorem Calculator
This calculator is designed to calculate unknown side lengths in right triangles using the Pythagorean Theorem.
This calculator is designed to calculate unknown side lengths in right triangles using the Pythagorean Theorem. Just enter the lengths of two sides of the right triangle and the calculator will give you the length of the third side. You can use this tool to explore the basic geometric relationships of right triangles and solve geometry problems.
When using the online Pythagorean Theorem calculator: by entering 1. edge and 2. edge you can calculate side a, side b or hypotenuse c.
Table of contents:
How to Work Pythagorean Theorem Calculator?
The Pythagorean Theorem states that in a right triangle, the sum of the squares of the right sides is equal to the square of the hypotenuse. So, in a right triangle, with A and B being the right sides and C being the hypotenuse, the theorem is expressed as follows:
C^2 = A^2 + B^2- c: represents the length of the hypotenuse (the longest side of a right triangle).
- a and b: represent the lengths of the right sides.
Step-by-Step Calculation:
- Determine the Right Sides: First, determine the right sides (A and B) of the right triangle.
- Square the Edges: Square the perpendicular sides A and B (A² and B²).
- Add them together: Find the sum of the squares (A² + B²).
- Take the Square Root: Take the square root to find the length of the hypotenuse from the result (C = √(A² + B²)).
Pythagorean Theorem Formula
The Pythagorean Theorem is represented by a mathematical formula:
C^2 = A^2 + B^2Uses of Pythagorean Theorem Calculator
- Construction and Engineering: It is used to determine right angles in structures.
- Astronomy and Geography: Used for distance calculations.
- Graphic Design and Computer Science: Pythagorean Theorem calculator can be used to calculate distances between pixels, determine diagonal measurements in UI layouts, or create precise geometric shapes and animations.
- Natural Sciences and Physics: Used for motion analysis.
Interesting Facts about the Pythagorean Theorem
These insights into the Pythagorean Theorem help us understand its historical significance and practical applications in daily life. ou can also find other useful math calculators here.