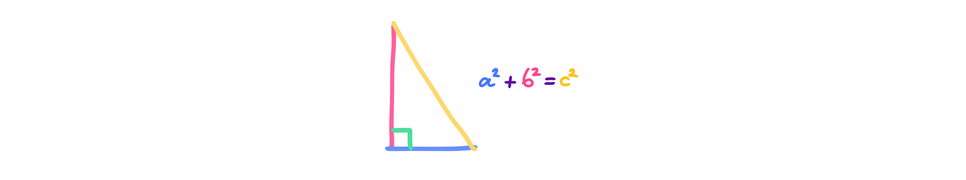Калькулятор теоремы Пифагора
Этот калькулятор предназначен для расчета неизвестных длин сторон прямоугольных треугольников с использованием теоремы Пифагора.
Этот калькулятор предназначен для расчета неизвестных длин сторон прямоугольных треугольников с использованием теоремы Пифагора. Просто введите длины двух сторон прямоугольного треугольника, и калькулятор выдаст вам длину третьей стороны. Вы можете использовать этот инструмент для изучения основных геометрических отношений прямоугольных треугольников и решения геометрических задач.
При использовании онлайн-калькулятора теоремы Пифагора: введя 1. ребро и 2. ребро, вы можете вычислить сторону a, сторону b или гипотенузу c.
Оглавление:
Как работать с калькулятором теоремы Пифагора?
Теорема Пифагора утверждает, что в прямоугольном треугольнике сумма квадратов правых сторон равна квадрату гипотенузы. Итак, в прямоугольном треугольнике, где A и B — правые стороны, а C — гипотенуза, теорема выражается следующим образом:
C^2 = A^2 + B^2- с: представляет длину гипотенузы (самой длинной стороны прямоугольного треугольника).
- а и б: обозначают длины правых сторон.
Пошаговый расчет:
- Определите правые стороны. Сначала определите правые стороны (A и B) прямоугольного треугольника.
- Выровняйте края: выровняйте перпендикулярные стороны A и B (A² и B²).
- Сложите их: найдите сумму квадратов (A² + B²).
- Извлеките квадратный корень. Извлеките квадратный корень, чтобы найти длину гипотенузы по результату (C = √(A² + B²)).
Формула теоремы Пифагора
Теорема Пифагора представлена математической формулой:
C^2 = A^2 + B^2Использование калькулятора теоремы Пифагора
- Строительство и инженерия: Используется для определения прямых углов в конструкциях.
- Астрономия и география: Используется для расчета расстояния.
- Графический дизайн и информатика: Калькулятор теоремы Пифагора можно использовать для расчета расстояний между пикселями, определения диагональных размеров в макетах пользовательского интерфейса или создания точных геометрических фигур и анимаций.
- Естественные науки и физика: Используется для анализа движения.
Интересные факты о теореме Пифагора
Эти взгляды на теорему Пифагора помогают нам понять ее историческое значение и практическое применение в повседневной жизни. Вы также можете найти другие полезные математические калькуляторы. здесь.