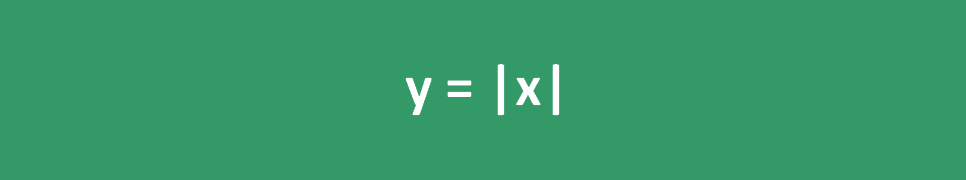Absolute Value Calculator

The Absolute Value Calculator quickly and easily calculates the absolute value of the number you enter. By entering any number, positive or negative, the calculator will show you its absolute value, the distance from zero. This online tool is the ideal solution to simplify your mathematical operations and make absolute value calculations quickly. Use our absolute value finder for your daily calculations.

How is Absolute Value Calculated with an Absolute Value Calculator?

Using an Absolute Value Calculator simplifies the process of finding the absolute value of any number. Absolute value is a value that indicates how far a number is from zero and is always expressed as positive. In mathematics, absolute value is usually represented by two vertical lines: |x|.

Definition of Absolute Value:

1. If a number is positive (x > 0), its absolute value is itself. |x| = x
2. If the number is zero (x = 0), its absolute value is zero. |0| = 0
3. If the number is negative (x < 0), its absolute value is the positive form of the number. |x| = -x

Examples:

• |5| = 5
• |-5| = 5
• |0| = 0

Applications of Absolute Value:

Absolute value is often used in mathematics and various sciences to calculate distances, differences and error rates. For example, absolute value is used to find the magnitude of the difference between two numbers. It is also often found in fields such as finance and engineering.

The absolute value function can also be represented by a graph like the one below: y = |x|

In this graph, points with negative values on the x-axis are reflected as positive on the y-axis and both sides of the graph are symmetric with respect to the y-axis.

What is Absolute Value?

In mathematics, absolute value is the distance of a number from zero and always takes a positive value. Absolute value is usually represented by placing vertical lines on either side of the number: |x|. Absolute value treats negative and positive numbers in the same way, because it is only the magnitude that matters, not the sign. Use our absolute value calculator to easily find the absolute value of any number.

Properties of Absolute Value:

• Positivity: The absolute value is always greater than or equal to zero.
• Symmetry: The absolute values of a number and its negative are the same. For example, |3| = 3 and |-3| = 3.
• Triangle Inequality: |a + b| ≤ |a| + |b|, this property is often used in algebraic operations.

Uses of Absolute Value:

Absolute value is used in various mathematical and scientific applications. In particular, it plays an important role in distance calculations, determining the magnitude of differences and error analysis. For example, the distance between two points is calculated as the sum of the absolute values of the differences of their coordinates.

The absolute value function is represented on a graph as y = |x|, which is symmetric with respect to the y-axis.

Absolute Value Calculation Methods

Absolute value indicates the distance of a number from zero and is frequently used in mathematical calculations. The methods used to calculate the absolute value are based on basic math rules. Our absolute value calculator automates these methods. You can find more mathematical calculators here.

1. Basic Method:

The following rules apply to calculate the absolute value:

• If a number is positive, its absolute value is itself. |x| = x (if x ≥ 0)
• If a number is negative, its absolute value is its positive form. |x| = -x (if x < 0)

Examples:

• The absolute value of a positive number: |8| = 8
• The absolute value of a negative number: |-8| = 8
• The absolute value of zero: |0| = 0

Calculation of Absolute Value by Algebraic Methods:

Absolute value can also be calculated in some mathematical operations and equations. Here are some common algebraic methods:

Absolute Value Equations:

|x + 3| = 7

This equation offers two different solutions:

• x = 4 if x + 3 = 7
• x = -10 if x + 3 = -7

Absolute Value Inequalities:

|x – 2| < 5

This inequality breaks down into the following two inequalities:

-5 < x – 2 < 5

This means that x < 7 and x > -3. Consequently -3 < x < 7

Triangle Inequality:

The absolute value of the sum of two numbers is less than or equal to the sum of their absolute values. |a + b| ≤ |a| + |b|

2. Graphical Method:

The absolute value function is represented on the graph as a V-shaped curve. The graph of the basic absolute value function is defined as y = |x| and is symmetric with a vertex at the origin. This graph has positive values on both sides of the x-axis.

3. Applied Methods:

Absolute value is often used in real-life distance calculations, error analysis and data science. For example, the distance between two points or the margin of error in a measurement are calculated with absolute value.

Methods for calculating absolute value play an important role in solving mathematical problems and developing analytical thinking skills.

Uses of Absolute Value in Daily Life

Absolute value is an important concept in mathematics and we encounter it in various fields in our daily lives. Remembering that the absolute value is a positive value that indicates the distance of a number from zero, we can explore its different uses.

1. Distance Calculations:

Absolute value is frequently used in distance calculations. For example, when finding the distance between two points, we take the absolute value of the difference of their coordinates. This ensures that the distance is always positive.

Example: When calculating the distance between two cities, the absolute value of their coordinate differences is used.

2. Error Analysis:

Absolute value is used when analyzing errors in measurements. The absolute value of the difference between the actual value and the measured value indicates the magnitude of the error.

Example: The absolute value of the difference between the temperature measured by a thermometer and the actual temperature gives the measurement error.

3. Finance and Economics:

In financial analysis, absolute value is used to determine the magnitude of gains or losses