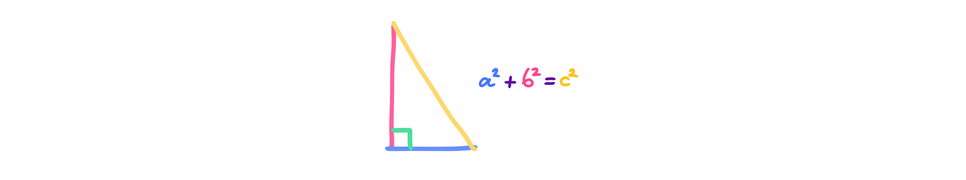Satz des Pythagoras-Rechner
Dieser Rechner dient zur Berechnung unbekannter Seitenlängen in rechtwinkligen Dreiecken mithilfe des Satzes des Pythagoras.
Dieser Rechner ist dafür ausgelegt, unbekannte Seitenlängen in rechtwinkligen Dreiecken mithilfe des Satzes des Pythagoras zu berechnen. Geben Sie einfach die Längen von zwei Seiten des rechtwinkligen Dreiecks ein und der Rechner berechnet Ihnen die Länge der dritten Seite. Mit diesem Tool können Sie die grundlegenden geometrischen Beziehungen rechtwinkliger Dreiecke erkunden und Geometrieprobleme lösen.
Bei Verwendung des Online-Satz-Rechners des Pythagoras gilt: Durch Eingabe der 1. Kante und der 2. Kante können Sie Seite a, Seite b oder Hypothenuse c berechnen.
Das Inhaltsverzeichnis:
Wie funktioniert der Satz-des-Pythagoras-Rechner?
Der Satz des Pythagoras besagt, dass in einem rechtwinkligen Dreieck die Summe der Quadrate der rechten Seiten gleich dem Quadrat der Hypothenuse ist. In einem rechtwinkligen Dreieck, bei dem A und B die rechten Seiten und C die Hypothenuse sind, wird der Satz also wie folgt ausgedrückt:
C^2 = A^2 + B^2- C: stellt die Länge der Hypothenuse dar (die längste Seite eines rechtwinkligen Dreiecks).
- A und B: stellen die Längen der rechten Seiten dar.
Schrittweise Berechnung:
- Bestimmen Sie die rechten Seiten: Bestimmen Sie zuerst die rechten Seiten (A und B) des rechtwinkligen Dreiecks.
- Kanten ausrichten: Richten Sie die senkrechten Seiten A und B (A² und B²) aus.
- Addiere sie: Ermittle die Summe der Quadrate (A² + B²).
- Ziehen Sie die Quadratwurzel: Ziehen Sie die Quadratwurzel, um die Länge der Hypothenuse aus dem Ergebnis (C = √(A² + B²)) zu ermitteln.
Formel des Satzes des Pythagoras
Der Satz des Pythagoras wird durch eine mathematische Formel dargestellt:
C^2 = A^2 + B^2Verwendungsmöglichkeiten des Pythagoras-Theorem-Rechners
- Bau und Ingenieurwesen: Es wird verwendet, um rechte Winkel in Strukturen zu bestimmen.
- Astronomie und Geographie: Wird für Entfernungsberechnungen verwendet.
- Grafikdesign und Informatik: Mit dem Rechner zum Satz des Pythagoras können Sie Abstände zwischen Pixeln berechnen, diagonale Maße in UI-Layouts bestimmen oder präzise geometrische Formen und Animationen erstellen.
- Naturwissenschaften und Physik: Wird zur Bewegungsanalyse verwendet.
Interessante Fakten zum Satz des Pythagoras
Diese Einblicke in den Satz des Pythagoras helfen uns, seine historische Bedeutung und seine praktischen Anwendungen im täglichen Leben zu verstehen. Sie können auch andere nützliche mathematische Rechner finden Hier.