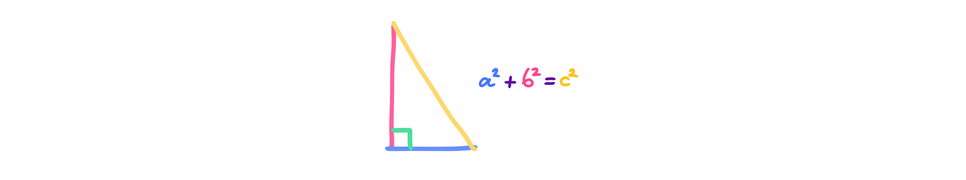حاسبة نظرية فيثاغورس
تم تصميم هذه الآلة الحاسبة لحساب أطوال الأضلاع غير المعروفة في المثلثات القائمة باستخدام نظرية فيثاغورس.
تم تصميم هذه الآلة الحاسبة لحساب أطوال الأضلاع غير المعروفة في المثلثات القائمة باستخدام نظرية فيثاغورس. ما عليك سوى إدخال طولي ضلعين من المثلث الأيمن وستعطيك الآلة الحاسبة طول الضلع الثالث. يمكنك استخدام هذه الأداة لاستكشاف العلاقات الهندسية الأساسية للمثلثات القائمة وحل المشكلات الهندسية.
عند استخدام حاسبة نظرية فيثاغورس عبر الإنترنت: عن طريق إدخال 1. الحافة و 2. الحافة، يمكنك حساب الضلع أ أو الضلع ب أو الوتر ج.
جدول المحتويات:
كيفية استخدام حاسبة نظرية فيثاغورس؟
تنص نظرية فيثاغورس على أن مجموع مربعات أضلاعه اليمنى في المثلث القائم يساوي مربع الوتر. لذا، في المثلث القائم الزاوية، حيث A وB هما الضلعان الأيمنان وC هو الوتر، يتم التعبير عن النظرية على النحو التالي:
C^2 = A^2 + B^2- ج: يمثل طول الوتر (أطول ضلع في المثلث القائم الزاوية).
- أ و ب: تمثل أطوال الجانبين الأيمن.
حساب خطوة بخطوة:
- تحديد الجوانب اليمنى: أولاً، حدد الجوانب اليمنى (أ وب) للمثلث القائم.
- تربيع الحواف: قم بتربيع الجوانب المتعامدة A وB (A² وB²).
- اجمعهما معًا: أوجد مجموع المربعات (A² + B²).
- خذ الجذر التربيعي: خذ الجذر التربيعي لإيجاد طول الوتر من النتيجة (C = √(A² + B²)).
صيغة نظرية فيثاغورس
يتم تمثيل نظرية فيثاغورس بالصيغة الرياضية التالية:
C^2 = A^2 + B^2استخدامات حاسبة نظرية فيثاغورس
- البناء والهندسة: يتم استخدامه لتحديد الزوايا القائمة في الهياكل.
- علم الفلك والجغرافيا: تستخدم لحساب المسافة.
- التصميم الجرافيكي وعلوم الكمبيوتر: يمكن استخدام حاسبة نظرية فيثاغورس لحساب المسافات بين وحدات البكسل، أو تحديد القياسات القطرية في تخطيطات واجهة المستخدم، أو إنشاء أشكال هندسية ورسوم متحركة دقيقة.
- العلوم الطبيعية والفيزياء: يستخدم لتحليل الحركة.
حقائق مثيرة للاهتمام حول نظرية فيثاغورس
تساعدنا هذه الأفكار حول نظرية فيثاغورس على فهم أهميتها التاريخية وتطبيقاتها العملية في الحياة اليومية. يمكنك أيضًا العثور على حاسبات رياضية مفيدة أخرى هنا.