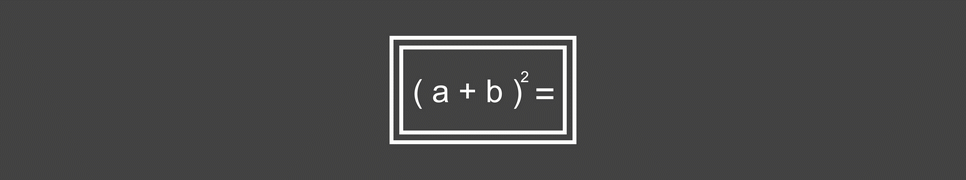Калькулятор экспоненты

Вы можете использовать наш калькулятор экспонент, чтобы быстро и точно выполнить возведение в степень, которое часто встречается в математике. Калькулятор экспоненты умножает число на определенную экспоненту и мгновенно показывает результат.

При использовании онлайн-калькулятора экспоненты: Вы можете выполнить расчет, введя «Основание (x)» и «Степень (n)».

Как рассчитывается показатель степени?

Возведение в степень — это процесс умножения числа на само себя определенное количество раз. Возведение в степень часто используется в математических операциях и применяется, когда необходимо определить или вычислить показатель степени числа.

Простое вычисление экспоненты

1. Определите базу: Сначала определите основание числа, которое нужно возвести в степень. Основание — это число, которое нужно возвести в степень.
2. Определите показатель: Далее определите, сколько показателей нужно взять. Показатель степени — это величина, указывающая, сколько раз нужно умножить число само на себя.
3. Процесс расчета: Наконец, умножьте основание числа само на себя на показатель степени. Например, чтобы вычислить 2^3, вам нужно умножить число 2 само на себя 3 раза: 2 x 2 x 2 = 8.

Примеры:

• Расчет 2^3: 2 x 2 x 2 = 8
• Расчет 3^2: 3 x 3 = 9
• Расчет 5^4: 5 x 5 x 5 x 5 = 625

Формула расчета экспоненты

Возведение в степень означает умножение числа само на себя определенное количество раз. Этот процесс математически представлен формулой ниже:

Формула расчета показателя: а^н

а: Базовый номер. Это число, которое нужно взять в степень.

n: Значение показателя. Это число, указывающее, сколько раз базовое число будет умножено само на себя.

Формула расчета экспоненты означает умножение заданного базового числа на заданное значение экспоненты. Например, выражение 2³ относится к процессу умножения 2 само на себя три раза.

Пример:

Рассмотрим расчет 2³:

a=2: базовое число
n=3: значение показателя степени

В этом случае выражение 2³ относится к операции умножения числа 2 само на себя три раза:

2³ = 2×2×2=8

Таким образом, вы можете легко вычислить любое основание числа, умноженное на любой показатель степени, используя формулу. Вы можете найти более подробную математическую информацию о математике здесь.

Понятие экспоненты и его важность в математике

В математике показатель степени — это процесс умножения числа само на себя определенное количество раз. Это понятие играет важную роль в математических расчетах и решении задач. Вот важные моменты понятия показателя степени в математике:

1. Основные математические расчеты: Возведение в степень является фундаментальной частью основных математических вычислений. Возведение в степень основано на умножении и может быть определено как процесс умножения числа само на себя определенное количество раз.
2. Упрощение сложных операций: Возведение в степень используется для упрощения сложных математических выражений. Возведение в степень больших чисел или выражений делает вычисления меньшими и более управляемыми.
3. Научное исследование: Понятие показателей часто используется в физике, химии, технике и других науках. В частности, возведение в степень используется для объяснения природных явлений, темпов роста, передачи энергии и других явлений.
4. Финансовые расчеты: В финансовом анализе концепция показателя важна для расчета доходности инвестиций и оценки будущей стоимости. Возведение в степень используется для расчета таких факторов, как процентные ставки и темпы роста.
5. Электроника и вычислительная техника: В области электроники и вычислительной техники концепция возведения в степень часто используется при анализе схем и построении алгоритмов. В частности, возведение в степень широко используется в операциях синхронизации и обработке данных.

Важность и области использования понятия показателя степени в математике широко распространены. Он эффективно используется во многих областях: от базовых математических расчетов до научных исследований, от финансового анализа до инженерных приложений.

Преимущества использования калькулятора экспоненты

Калькулятор экспоненты дает множество преимуществ, помимо быстрого и точного выполнения математических расчетов. Вот некоторые преимущества использования калькулятора экспонент:

• Быстрые и точные расчеты: Калькуляторы экспонент быстро и точно выполняют сложные возведения в степень. Это быстрее, чем расчет вручную, и снижает вероятность ошибок.
• Экономия времени: Калькулятор экспонент экономит время, быстро выполняя математические операции. Это экономит время, особенно когда необходимо возвести в степень большие числа или сложные выражения.
• Легко использовать: Калькуляторы экспонент обычно имеют простой в использовании интерфейс. Простой ввод значений основания и показателя степени позволяет сразу получить результат.
• Может использоваться как средство обучения: Калькулятор экспоненты может помочь учащимся в процессе изучения математики. Его можно использовать как интерактивный инструмент для лучшего понимания и применения математических концепций.
• Его можно использовать в различных математических операциях: Калькулятор возведения в степень часто можно использовать не только для возведения в степень, но и для вычисления корневых выражений и других математических операций.
• Профессиональное и академическое использование: Калькулятор возведения в степень может использоваться многими людьми, от студентов до профессионалов, для академических и профессиональных расчетов. Он широко используется в финансах, технике, науке и других областях.

Преимущества использования калькулятора экспонент позволяют выполнять математические операции более эффективно и результативно.