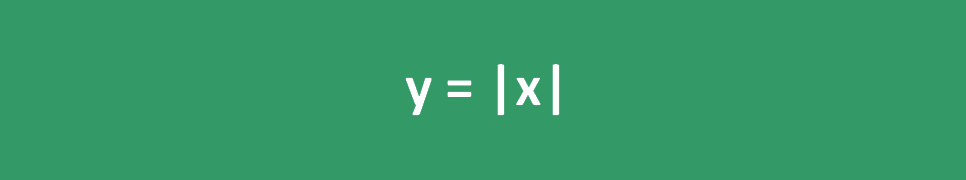Absolutwertrechner

Der Absolutwertrechner Berechnet schnell und einfach den Absolutwert der eingegebenen Zahl. Durch Eingabe einer beliebigen Zahl, ob positiv oder negativ, zeigt Ihnen der Rechner den Absolutwert, den Abstand von Null, an. Dieses Online-Tool ist die ideale Lösung, um Ihre mathematischen Operationen zu vereinfachen und absoluter Wert Berechnungen schnell. Nutzen Sie unsere Absolutwertfinder für Ihre täglichen Berechnungen.

Wie wird der Absolutwert mit einem Absolutwertrechner berechnet?

Mit einem Absolutwertrechner Vereinfacht die Berechnung des Betrags einer Zahl. Der Betrag gibt an, wie weit eine Zahl von Null entfernt ist und ist immer positiv. In der Mathematik wird der Betrag üblicherweise durch zwei vertikale Linien dargestellt: |x|.

Definition des Absolutwerts:

1. Wenn eine Zahl positiv ist (x > 0), ist ihr Absolutwert sie selbst. |x| = x
2. Wenn die Zahl Null ist (x = 0), ist ihr Absolutwert Null. |0| = 0
3. Wenn die Zahl negativ ist (x < 0), ist ihr Absolutwert die positive Form der Zahl. |x| = -x

Beispiele:

• |5| = 5
• |-5| = 5
• |0| = 0

Anwendungen des Absolutwerts:

Der Absolutwert wird häufig in der Mathematik und in verschiedenen Wissenschaften verwendet, um Entfernungen, Unterschiede und Fehlerquoten zu berechnen. Zum Beispiel wird der Absolutwert verwendet, um die Größe des Unterschieds zwischen zwei Zahlen zu ermitteln. Er wird auch häufig in Bereichen wie Finanzen und Ingenieurwesen gefunden.

Die Absolutwertfunktion kann auch durch ein Diagramm dargestellt werden, wie das untenstehende: y = |x|

In diesem Diagramm werden Punkte mit negativen Werten auf der x-Achse als positive auf der y-Achse gespiegelt, und beide Seiten des Graphen sind bezüglich der y-Achse symmetrisch.

What is Absolute Value?

In der Mathematik absoluter Wert ist der Abstand einer Zahl von Null und nimmt immer einen positiven Wert an. Der Betrag wird üblicherweise durch vertikale Striche an beiden Seiten der Zahl dargestellt: |x|. Der Betrag behandelt negative und positive Zahlen gleich, da nur der Betrag zählt, nicht das Vorzeichen. Verwenden Sie unsere Absolutwertrechner um einfach den Absolutwert einer beliebigen Zahl zu finden.

Eigenschaften des Absolutwerts:

• Positivität: Der Absolutwert ist immer größer oder gleich null.
• Symmetrie: Die Absolutwerte einer Zahl und ihrer negativen Form sind gleich. Zum Beispiel, |3| = 3 und |-3| = 3.
• Dreiecksungleichung: |a + b| ≤ |a| + |b|, diese Eigenschaft wird häufig in algebraischen Operationen verwendet.

Verwendungen des Absolutwerts:

Der Absolutwert wird in verschiedenen mathematischen und wissenschaftlichen Anwendungen verwendet. Insbesondere spielt er eine wichtige Rolle bei der Berechnung von Entfernungen, der Bestimmung der Größe von Unterschieden und der Fehleranalyse. Zum Beispiel wird die Entfernung zwischen zwei Punkten als Summe der Absolutwerte der Unterschiede ihrer Koordinaten berechnet.

Die Absolutwertfunktion wird auf einem Graphen als y = |x| dargestellt, der bezüglich der y-Achse symmetrisch ist.

Methoden zur Berechnung des Absolutwerts

Absoluter Wert gibt den Abstand einer Zahl von Null an und wird häufig in mathematischen Berechnungen verwendet. Die Methoden zur Berechnung des Betrags basieren auf grundlegenden mathematischen Regeln. Unsere Absolutwertrechner automatisiert diese Methoden. Weitere mathematische Rechner finden Sie Hier.

1. Grundmethode:

Die folgenden Regeln gelten zur Berechnung des Absolutwerts:

• Wenn eine Zahl positiv ist, ist ihr Absolutwert sie selbst. |x| = x (wenn x ≥ 0)
• Wenn eine Zahl negativ ist, ist ihr Absolutwert ihre positive Form. |x| = -x (wenn x < 0)

Beispiele:

• Der Absolutwert einer positiven Zahl: |8| = 8
• Der Absolutwert einer negativen Zahl: |-8| = 8
• Der Absolutwert von Null: |0| = 0

Berechnung des Absolutwerts durch algebraische Methoden:

Der Absolutwert kann auch in einigen mathematischen Operationen und Gleichungen berechnet werden. Hier sind einige gängige algebraische Methoden:

Absolutwertgleichungen:

|x + 3| = 7

Diese Gleichung bietet zwei verschiedene Lösungen:

• x = 4 wenn x + 3 = 7
• x = -10, wenn x + 3 = -7

Ungleichungen mit Absolutwerten:

|x – 2| < 5

Diese Ungleichung wird in die folgenden zwei Ungleichungen aufgeteilt:

-5 < x – 2 < 5

Dies bedeutet, dass x < 7 und x > -3. Folglich -3 < x < 7

Dreiecksungleichung:

Der Absolutwert der Summe zweier Zahlen ist kleiner oder gleich der Summe ihrer Absolutwerte. |a + b| ≤ |a| + |b|

2. Grafische Methode:

Die Absolutwertfunktion wird im Graphen als V-förmige Kurve dargestellt. Der Graph der grundlegenden Absolutwertfunktion ist definiert als y = |x| und ist symmetrisch mit einem Scheitelpunkt am Ursprung. Dieser Graph hat auf beiden Seiten der x-Achse positive Werte.

3. Angewandte Methoden:

Der Absolutwert wird häufig in realen Entfernungsberechnungen, Fehleranalysen und der Datenwissenschaft verwendet. Zum Beispiel wird die Entfernung zwischen zwei Punkten oder der Fehlerbereich in einer Messung mit dem Absolutwert berechnet.

Methoden zur Berechnung des Absolutwerts spielen eine wichtige Rolle bei der Lösung mathematischer Probleme und der Entwicklung analytischer Denkfähigkeiten.

Verwendungen des Absolutwerts im täglichen Leben

Absoluter Wert ist ein wichtiges Konzept in der Mathematik und begegnet uns in verschiedenen Bereichen unseres täglichen Lebens. Wenn wir uns daran erinnern, dass der Betrag ein positiver Wert ist, der den Abstand einer Zahl von Null angibt, können wir seine verschiedenen Verwendungsmöglichkeiten erkunden.

1. Entfernungsberechnungen:

Der Absolutwert wird häufig in Entfernungsberechnungen verwendet. Zum Beispiel, wenn man die Entfernung zwischen zwei Punkten berechnet, nimmt man den Absolutwert der Differenz ihrer Koordinaten. Dadurch wird sichergestellt, dass die Entfernung immer positiv ist.

Beispiel: Bei der Berechnung der Entfernung zwischen zwei Städten wird der Absolutwert ihrer Koordinatendifferenzen verwendet.

2. Fehleranalyse:

Der Absolutwert wird bei der Analyse von Fehlern in Messungen verwendet. Der Absolutwert der Differenz zwischen dem tatsächlichen Wert und dem gemessenen Wert zeigt die Größe des Fehlers an.

Beispiel: Der Absolutwert der Differenz zwischen der mit einem Thermometer gemessenen Temperatur und der tatsächlichen Temperatur gibt den Messfehler an.

3. Finanzen und Wirtschaft:

In der Finanzanalyse wird der absolute Wert verwendet, um das Ausmaß von Gewinnen oder Verlusten zu bestimmen